Turtle is like a drawing board.

It has functions like forward(...) and left(...) which can move the turtle around.

from turtle import *

forward(25)

left(30)

The forward(...) function takes the number of pixels which you want to move forward, left(...) takes a number of degrees which you want to rotate to the left. (There are backward(...) and right(...), too.)

---

Exercise: Draw a square as in the following picture:

For a square you will probably need a right angle, which is 90 degrees.

Solution:

from turtle import *
forward(50)
left(90)
forward(50)
left(90)
forward(50)
left(90)
forward(50)
left(90)

Bonus:

If you want to get creative, you can modify your shape with the width(...) and color(...) functions. If you cannot figure out the signature of a function (that is the syntax and semantics of it, say, number of parameters and their meaning) you can use help(color).

---

Exercise:

Can you draw a (non-square) rectangle too?

Solution:

from turtle import *
forward(100)
left(90)
forward(50)
left(90)
forward(100)
left(90)
forward(50)
left(90)

Bonus:

How about a triangle? (A triangle with 120 degrees angles will have all legs equally sized.)

---

Exercise:

Now, draw a tilted square. And another one, and another one. You can experiment with the angles between the individual squares.

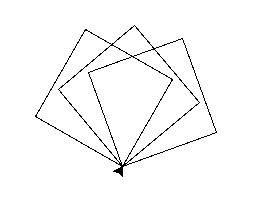
Try 20, 90 and 180 for example.

Solution:

from turtle import *

left(20)     # <--

forward(50)
left(90)
forward(50)
left(90)
forward(50)
left(90)
forward(50)
left(90)

left(20)     # <--

forward(50)
left(90)
forward(50)
left(90)
forward(50)
left(90)
forward(50)
left(90)

left(20)     # <--

forward(50)
left(90)
forward(50)
left(90)
forward(50)
left(90)
forward(50)
left(90)

Whew. Experimenting with the angles requires you to change three different places each time. Imagine you'd want to experiment with the square sizes, let alone with rectangles! We can do better than that.

---

This is where names come into play: You can tell Python that from now on, whenever you refer to a name, you actually mean something else. That concept might be familiar from symbolic maths, where you would write: Let x be 5. Then x*2 will obviously be 10. That's why those names are known as variables, too.

In Python syntax, that very statement translates to:

x = 5

After that statement, if you do print x, it will actually output its value --- 5. You can well use that for turtle too:

forward(x)

---

Exercise:

If we have a variable called angle, how could we use that to experiment much faster with our tilted squares program?

Solution:

from turtle import *
angle = 20

left(angle)

forward(50)
left(90)
forward(50)
left(90)
forward(50)
left(90)
forward(50)
left(90)

left(angle)
# ...

Bonus:

Can you apply that principle to the size of the squares, too?

---

Exercise:

Draw a house.

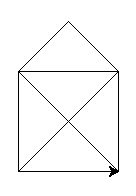
You can calculate the length of the diagonal line with Pythagoras. That value is a good candidate for a name binding.

---

There is still a lot of duplicated code --- the actual drawing of the rectangle --- around. If you need to copy and paste code, that is usually a sign of lacking abstractions. (Programmers call it a code smell.)

Functions are one way to express abstractions in Python. Let's take reset() for example. It is actually an abstraction for a number of steps, namely:

• Erase the drawing board
• Set the width and color back to default
• Move the turtle back to its initial position

A function can be defined with the def keyword in Python:

def line_without_moving():
  forward(50)
  backward(50)

You can access names in functions as well:

size = 50
def line_without_moving():
  forward(size)
  backward(size)

---

Exercise:

Write a function that draws a square. Can you see how you could improve the tilted squares program with that and greatly relieve experimentation?

---

Exercise:

Write a function that draws a hexagon.

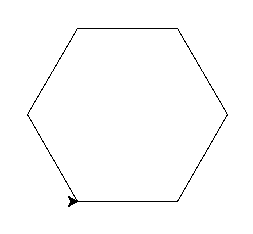
Now combine that function into a honeycomb.

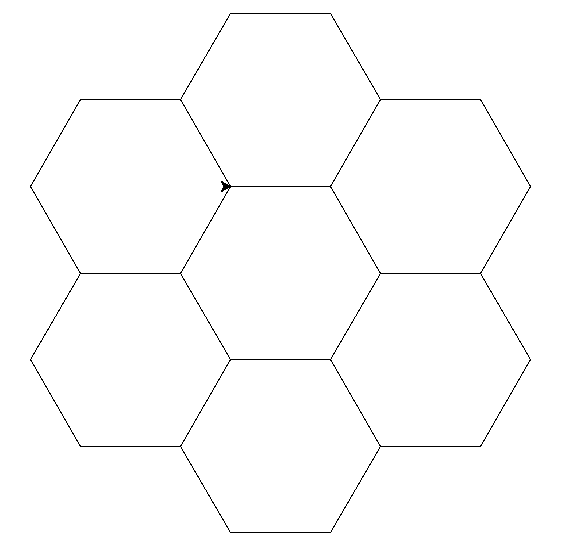
Solution:

def hexagon():
    forward(100)
    left(60)
    forward(100)
    left(60)
    forward(100)
    left(60)
    forward(100)
    left(60)
    forward(100)
    left(60)
    forward(100)
    left(60)

hexagon()
forward(100)
right(60)

hexagon()
forward(100)
right(60)

hexagon()
forward(100)
right(60)

hexagon()
forward(100)
right(60)

hexagon()
forward(100)
right(60)

hexagon()
forward(100)
right(60)

---

One more thing: Our programs often featured repetition. There is a powerful concept in Python called looping, which we will elaborate later on. For now, take that easy example:

for i in range(10):
    print "Hello!"

---

Exercise:

Draw a dashed line. You can move the turtle without tracing a line behind you with the up() function; put it back on the ground with down().

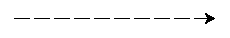
Solution:

for i in range(10):
    forward(15)
    up()
    forward(5)
    down()

Bonus:

Can you make the dashes become larger as the line progresses?

---

Exercise:

Take your honeycomb program and make it easier with loops. How small can you get it?

Solution:

def hexagon():
    for i in range(6):
        forward(100)
        left(60)

for i in range(6):
  hexagon()
  forward(100)
  right(60)